Lecture 12: First-class Functions
1 First-class Functions
In Lecture 8: Local Function Definitions and Tail Calls and Lecture 9: Global Function Definitions and Non-tail Calls, we introduced the ability for our programs to define functions that we could then call in other expressions in our program. Our programs were a sequence of function definitions, followed by one main expression. This notion of a program was far more flexible than we had before, and lets us define many computations we simply could not previously do. But it is distinctly unsatisfying: functions are second-class entities in our language, and can’t be used the same way as other values in our programs.
We know from other courses, and possibly even from using features like
iterators in Rust, that higher-order functions —
def applyToFive(it):
it(5)
in
def incr(x):
x + 1
in
applyToFive(incr)Do Now!
What errors currently get reported for this program?
Because it is a parameter to the first function, our compiler will
complain that it is not defined as a function, when used as such on line
2. Additionally, because incr is defined as a function, our compiler will
complain that it can’t be used as a parameter on the last line. We’d like to
be able to support this program, though, and others more sophisticated. Doing
so will bring in a number of challenges, whose solutions are detailed and all
affect each other. Let’s build up to those programs, incrementally.
2 Reminder: How are functions currently compiled?
Let’s simplify away the higher-order parts of the program above, and look just at a basic function definition. The following program:
def incr(x):
x + 1
end
incr(5)is compiled to something like1ignoring tag checking and tail call elimination:
incr:
mov RAX, [RSP - 8] ;; get param
add RAX, 2 ;; add (encoded) 1 to it
ret ;; exit
start_here:
mov [RSP - 16], 10 ;; pass 5 as an argument
call incr ;; call function
ret ;; exitThis compilation is a pretty straightforward translation of the code we have. What can we do to start supporting higher-order functions?
3 The value of a function —
3.1 Passing in functions
Going back to the original motivating example, the first problem we encounter is seen in the first and last lines of code.
def applyToFive(it):
it(5)
in
def incr(x):
x + 1
in
applyToFive(incr)Functions receive values as their parameters, and function calls push values
onto the stack. So in order to “pass a function in” to another function, we
need to answer the question, what is the value of a function? In the
assembly above, what could possibly be a candidate for the value of the
incr function?
A function, as a standalone entity, seems to just be the code that comprises its compiled body. We can’t conveniently talk about the entire chunk of code, though, but we don’t actually need to. We really only need to know the “entrance” to the function: if we can jump there, then the rest of the function will execute in order, automatically. So one prime candidate for “the value of a function” is the address of its first instruction. Annoyingly, we don’t know that address explicitly, but fortunately, the assembler helps us here: we can just use the initial label of the function, whose name we certainly do know. This is basically what in C/C++ we would call a function pointer.
In other words, we can compile the main expression of our program as:
start_here:
mov RAX, incr ;; load the address of incr into RAX
mov [RSP - 16], RAX ;; pass the address of incr as an argument
call applyToFive ;; call function
ret ;; exitThis might seem quite bizarre: how can we mov a label into a
register? Doesn’t mov require that we mov a value —calling a label in the first
place: the assembler replaces those named labels with the actual
addresses within the program, and so at runtime, they’re simply normal
QWORD values representing memory addresses. Note that we can’t
do this in one expression mov [RSP - 16], incr because the
incr is a 64-bit address and x64 doesn’t support moving a
64-bit literal into a memory location, so we need the intermediate
register.
3.2 Using function arguments
Do Now!
The compiled code for
applyToFivelooks like this:applyToFive: mov RAX, [RSP - 8] ;; get the param mov ???? ;; pass the argument to `it` call ???? ;; call `it` ret ;; exitFill in the questions to complete the compilation of
applyToFive.
The parameter for it is simply 5, so we pass
10 as an argument on the stack, just as before. The function to
be called, however, isn’t identified by its label: we already have its
address, since it was passed in as the argument to
applyToFive. Accordingly, we call RAX in order to
find and call our function. Again, this generalizes the syntax of
call instructions slightly just as push was generalized:
we can call an address given by a register, instead of just a
constant.
3.3 Victory!
We can now pass functions to functions! Everything works exactly as intended.
Do Now!
Tweak the example program slightly, and cause it to break. What haven’t we covered yet?
4 The measure of a function —
Just because we use a parameter as a function doesn’t mean we actually
passed a function in as an argument. If we change our program to
applyToFive(true), our program will attempt to apply true as a
function, meaning it will try to call 0xFFFFFFFFFFFFFFFF, which isn’t likely to
be a valid address of a function.
As a second, related problem: suppose we get bored of merely incrementing values by one, and generalize our program slightly:
def applyToFive(it):
it(5)
in
def add(x, y):
x + y
in
applyToFive(add)Do Now!
What happens now?
Let’s examine the stack very carefully. When our program starts, it moves
add onto the stack, then calls applyToFive:

That function in turn moves 10 onto the stack, and calls
it, which in this case is add:
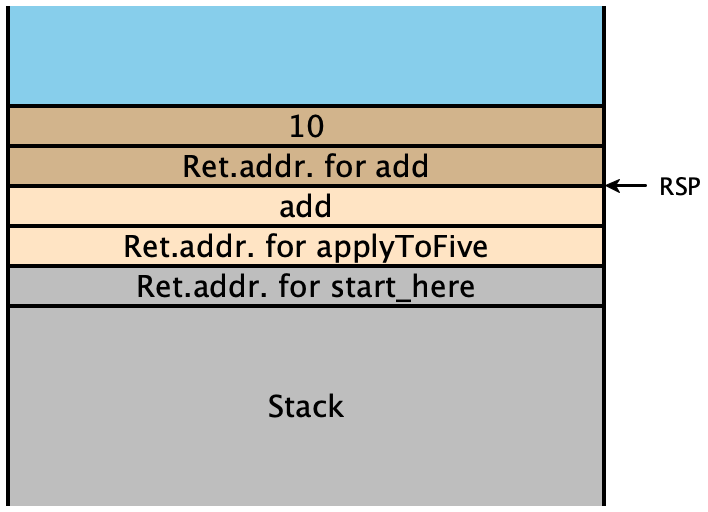
But look, since add has been called with only one argument, it
will read from the free stack space in blue for its second
argument. So it adds 5 (encoded as 10) to an
arbitrary unspecified value, since as far as it knows that stack
location is where its second parameter should be.
We had eliminated both of these problems before via well-formedness checking: our function-definition environment knew about every function and its arity, and we could check every function application to ensure that a well-known function was called, with the correct number of arguments were passed. But now that we can pass functions around dynamically, we can’t know statically whether the arities are correct, and can’t even know whether we have a function at all!
We don’t know anything about precisely where a function’s code begins, so there’s no specific property we could check about the value passed in to determine if it actually is a function. But in any case, that value is insufficient to encode both the function and its arity. Fortunately, we now have a technique for storing multiple pieces of data as a single value: tuples. So our second candidate for “the value of a function” is a tuple containing the function’s arity and start address. This isn’t quite right either, since we wouldn’t then be able to distinguish actual tuples from “tuples-that-are-functions”.
So we choose a new tag value, say 0x3, distinct from the ones
used so far, to mark these function values. Even better: we now have
free rein to separate and optimize the representation for functions,
rather than hew completely to the tuple layout. As one immediate
consequence: we don’t need to store the tuple length —
Do Now!
Revise the compiled code of
applyToFiveto assume it gets one of the new tuple-like values.
The pseudocode for calling a higher-order function like this is roughly:
mov RAX, <the function tuple> ;; load the intended function
<check-tag RAX, 0x3> ;; ensure it has the right tag
sub RAX, 3 ;; untag the value
<check-arity [RAX], num-args> ;; the second word at stores the arity
<push all the args> ;; set up the stack
call [RAX + 8] ;; the first word stores the function address
add RSP, <8 * num-args> ;; finish the callNow we just need to create these tuples.
Exercise
Revise the compiled code above to allocate and tag a function value using this new scheme, instead of a bare function pointer.
5 A function by any other name —
While everything above works fine for top-level, global function definitions, how do we extend it to our local function definitions?
To start, let’s consider the simple case of non-recursive functions. If the function is not recursive, then we don’t need our FunDefs form at all: instead we can use a literal notation for functions, the same way that we can write boolean, number and array literals. You may be familiar with these from other languages: we call them lambda expressions, and they appear in pretty much all modern major languages:
Language |
| Lambda syntax |
Javascript |
|
|
C++ |
|
|
Rust |
|
|
Ocaml |
|
|
We can rewrite any program using only non-recursive functions using lambdas instead as follows:
let applyToFive = (lambda it: it(5) end) in
let incr = (lambda x: x + 1 end) in
applyToFive(incr)Then, all our functions are defined in the same manner as any other let-binding: they’re just another expression, and we can simply produce the function values right then, storing them in let-bound variables as normal.
Now let’s consider what happens when we try to extend our lambda lifting procedure from diamondback to this new form on the following illustrative program:
let f =
if read_bool():
let seven = 7 in lambda x: x + seven end
else:
lambda y: y + 1
in
f(5)Here let’s assume we have implemented a new built-in function
read_bool that reads a boolean from stdin. Then we can’t
determine at compile time which branch of the if will be
taken, depending on whether the user inputs true or
false, we will either add seven or add one to 5. This
program makes perfect sense, but notice that if we naively apply our
lambda lifting, we run into a problem. Previously, we added each
captured variable as an extra argument, so if we did the same thing
here we would get the following, where we make up names for the
anonymous lambda functions:
def lambda1(seven, x): x + seven and
def lambda2(y): y + 1 in
let f = if read_bool(): (let seven = 7 in lambda1) else: lambda2
in
f(5)But we run into a problem: now lambda1 takes two arguments
but lambda2 takes one. Additionally, if
read_bool returns true we will call
lambda1 with only one argument, neglecting to "capture"
seven in any meaningful sense. Before we would have solved this by
adding seven to every place where lambda1 was
called, but now that functions are values that isn’t really
possible. And anyway, this call to f would need to be
applied to a different number of arguments when it calls
lambda1 vs lambda2. And if it seems like we
might be able to solve this by a sufficiently advanced analysis,
consider the fact that first class function values might be passed in
as arguments so it is not feasible to statically detect which captured
variables will be needed at each call site statically.
So instead, we will have to determine which extra arguments to pass dynamically, by including them as a third field in our function values. That is, our function values will now consist of an arity, a function pointer, and finally a (pointer to) an array of all the values captured by that function. This data structure is called a closure and we say it "closes over" the captured free variables. Then when we do lambda lifting, instead of adding each variable as an additional argument, we will package them up into an array, which we pass as a single argument. Then when we create a function value, we will pair up the function pointer and arity with an array of all the captured variables. We’ll do this by augmenting our intermediate representation with a new form for creating closures, analogous to our form for creating arrays:
def lambda1(env, x): let seven = env[0] in x + seven and
def lambda2(env, y): y + 1 in
let f = if read_bool():
(let seven = 7 in make_closure(1, lambda1, [seven]))
else:
make_closure(1, lambda2, [])
in
f(5)So now the captured variables are all stored in the single environment
parameter, and before we run the body, we project out all of the
captured free variables. Also notice that f(5) will need
to be compiled differently as f is not a statically known
function definition, but instead a dynamically determined closure
value.
Exercise
Augment your lambda lifting code to create make closures.
5.1 Compiling make_closure and function calls
Now that we have desugared away lambdas, we instead need to generate code to create closures at runtime. But we already know how to create heap-allocated values, we simply:
Move the arity, function pointer and environment into the next three available slots in the heap
Increment the heap pointer by 8 * 3
Return the previous value of the heap pointer, tagged with our closure tag 0x3
Correspondingly, we also need to change the way we implement function calls, but this will again be very similar to what we’ve already done with function calls in diamondback combined with code for reading from the heap:
Retrieve the function value, and check that it’s tagged as a closure.
Check that the arity matches the number of arguments being applied.
Call the code-label as before, but where the environment is passed as an additional first argument.
We can support both tail and non-tail calls in essentially the same way as before, the only difference is that the captured environment is always passed as the first argument and the address of the code we jump to is loaded from memory rather than a known static label.
6 Recursion
If we try even a simple recursive function —
let fac = (lambda n:
if n < 1: 1
else: n * fac(n - 1)) # ERROR: fac is not in scope
in fac(5)To accommodate this we’ll continue to support our old syntax for mutually recursive function definitions. But then we need to see how to extend our lambda lifting to support mutually recursive closures. There are many ways to implement this. Here is a fairly direct one. Alternatives include Landin’s knot and the Y combinator.
Given a mutually recursive function definition,
let x1 = e1,
x2 = e2,
x3 = e3 in
def f(x,y): e4
and
def g(a,b,c): e5
in
e6We need to lambda lift the function definitions, but also we need to
create closures for each of the functions in the body of the code we
leave behind, so the defs will get replaced by
lets where we use make_closure. Since all of
the functions are defined simultaneously, they all close over the same
environment, so we can create one environment and re-use it for each
of the closures we construct:
def f(env, x, y):
let x1 = env[0],
x2 = env[1],
x3 = env[2]
in e4'
and
def g(env, a, b, c):
let x1 = env[0],
x2 = env[1],
x3 = env[2]
in e5'
in
let x1 = e1',
x2 = e2',
x3 = e3',
env = [x1, x2, x3],
f = make_closure(2, f, env),
g = make_closure(3, g, env),
in
e6Do Now!
There is a bug in this translation! Can you find it?
We can’t forget that since f and g are
mutually recursive, they can use each other as first-class values, so
in the body of each function we should additionally create closures
for all of the mutually defined functions:
def f(env, x, y):
let x1 = env[0],
x2 = env[1],
x3 = env[2],
f = make_closure(2, f, env),
g = make_closure(3, g, env),
in e4'
and
def g(env, a, b, c):
let x1 = env[0],
x2 = env[1],
x3 = env[2]
f = make_closure(2, f, env),
g = make_closure(3, g, env),
in e5'
in
let x1 = e1',
x2 = e2',
x3 = e3',
env = [x1, x2, x3],
f = make_closure(2, f, env),
g = make_closure(3, g, env),
in
e6Do Now!
There is a memory leak in this translation! Can you find it?
The above translation uses unnecessary memory: each time a (recursive) function is called, it allocates a new closure on the heap. Since we haven’t implemented a garbage collector, this memory will never be reclaimed and our implementation will run out of heap memory when we write recursive programs.
How can we fix this? Well, notice that the closures we make in the
body of each function will be the same every time, since they are only
determined by the environment, so what if we tried to include the
closures f and g as part of the environment
env?
def f(env, x, y):
let x1 = env[0],
x2 = env[1],
x3 = env[2],
f = env[3],
g = env[4]
in e4'
and
def g(env, a, b, c):
let x1 = env[0],
x2 = env[1],
x3 = env[2],
f = env[3],
g = env[4]
in e5'
in
let x1 = e1',
x2 = e2',
x3 = e3',
env = [x1, x2, x3, f, g],
f = make_closure(2, f, env),
g = make_closure(3, g, env),
in
e6Do Now!
What went horribly wrong?
Wait, we are trying to put f and g in the
environment, but f and g are closures and
env is the environment part of their closure. So we have a
circular dependency: we need the closures f and
g to be implemented to create the environment
env, but we need the environment to construct the
closures! So we need a cycle in the heap.
But we know from previous classes how to make cycles in the heap using
mutation: we can start with a null pointer and then update it later to
make a cycle. We can similarly here initialize env with
some kind of "null pointers" in place of f and
g, then construct the closures and then "back-patch" the
environment to point to the newly created closures, making a cycle.
What do I mean by a "null pointer" though? Well we can just initialize
the element of the array to be any value, and then mutate it
later. Let’s use 0 to emphasize that it’s like a null
pointer:
def f(env, x, y):
let x1 = env[0],
x2 = env[1],
x3 = env[2],
f = env[3],
g = env[4]
in e4'
and
def g(env, a, b, c):
let x1 = env[0],
x2 = env[1],
x3 = env[2],
f = env[3],
g = env[4]
in e5'
in
let x1 = e1',
x2 = e2',
x3 = e3',
env = [x1, x2, x3, 0, 0],
f = make_closure(2, f, env),
g = make_closure(3, g, env),
in
env[3] := f;
env[4] := g;
e6Why does this work? Well notice that we won’t ever run the code
for f or g until we evaluate e6,
and so by the time f or g actually get’s
called, when it projects out env[3], it will have been
updated to point back to f itself. And we’ve solved the
original memory leak because now we only construct the closures for
f and g once.
Exercise
Extend the compilation above to work for recursive functions