Lecture 3: Let-bindings and simple stack allocations

1 Recap and refactoring

Last time, we considered the following miniscule language:

‹expr›: NUMBER

Our abstract syntax was simply

type expr = int64

and our compiler simply placed that integer in the appropriate place in the assembly. But let’s clean up that code somewhat: for a given number (let’s say 483), we generated the following assembly:

section .text
global start_here
start_here:
  mov RAX, 483
  ret

Of all of that code, only one line corresponds to our input program – the rest is scaffolding. Let’s refactor our compiler into two pieces, as follows:

enum Reg {
    Rax,
}

pub enum Instr {
    Mov(Reg, i64),
}

fn instrs_to_string(is: &[Instr]) -> String {
  /* do something to get a string of assembly */
}

/* compile_expr is responsible for compiling just a single expression,
   and does not care about the surrounding scaffolding */
fn compile_to_instrs(e: &Exp) -> Vec<Instr> {
  vec![ Instr::Mov(Reg::Rax, *e)]
}

/* compile_to_string surrounds a compiled program by whatever scaffolding is needed */
fn compile_to_string(e: &Exp) -> String {
    Ok(format!("\
        section .text
        global start_here
start_here:
{}
", instrs_to_string(&compile_to_instrs(e))))
}

This is a bit more code than we previously had, but it’s much more usefully organized: compile_to_string isn’t going to change 1For a little while! The details of this function will get more elaborate, and we’ll actually wrap this function in a larger pipeline, but the overall signature and purpose of the function will remain unchanged., and compile_to_instrs will simply grow to accomodate more elaborate expression forms.

2 Growing the language: adding (and subtracting) 1

Every time we enhance our source language, we need to consider several things:

1. Its impact on the concrete syntax of the language

2. Examples using the new enhancements, so we build intuition of them

3. Its impact on the abstract syntax and semantics of the language

4. Any new or changed transformations needed to process the new forms

5. Executable tests to confirm the enhancement works as intended

Let’s start by adding increment and decrement operations to our language.

2.1 The new concrete syntax

‹expr›: | NUMBER | add1 ( ‹expr› ) | sub1 ( ‹expr› )

2.2 Examples

These are not just example programs in the new language, but pairs of example programs and their intended behavior:

2.3 Enhancing the abstract syntax

pub enum Exp {
    Num(i64),
    Add1(Box<Exp>),
    Sub1(Box<Exp>),
}

Based on the examples above, the semantics for add1 and sub1 should be fairly obvious: they evaluate their argument to a number, and add or subtract one from it.

Exercise

Design an interpreter for this language. What should its signature be, and why?

2.4 Enhancing the transformations

To compile addition and subtraction, we need to enhance our knowledge of assembly. We’ll introduce one new instruction: add <dest>, <val> will increment the destination by the right-side value. (This mutates the destination, so if we still need the old value, we’ll need to have saved it somewhere else, first.) We’ll correspondingly enhance our definition of Instr to represent this new form:

enum Instr {
  ...
  Add(Reg, i32) /* Increment the left-hand reg by the value of the right-hand immediate */
  // In x86 only 32-bit literals can be on the right side of an add instruction
}

Do Now!

Given this new instruction, work out the desired assembly for the examples above.

Let’s consider the second example: add1(42). To compile this, we should load 42 into RAX, and then add 1 to it. Or in symbols,

mov RAX, 42
add RAX, 1

The last example is similar: given ~hl:4:s~sub1(~hl:3:s~add1(~hl:2:s~add1(~hl:1:s~42~hl:1:e~)~hl:2:e~)~hl:3:e~)~hl:4:e~, we want to load 42, then add 1 to it, then add 1 to that, then subtract 1 from that result. We currently only have add, though, so we’ll add -1 instead of subtracting:

~hl:1:s~mov RAX, 42~hl:1:e~
~hl:2:s~add RAX, 1~hl:2:e~
~hl:3:s~add RAX, 1~hl:3:e~
~hl:4:s~add RAX, -1~hl:4:e~

Notice how each piece of the input program corresponds to a related piece of the output assembly.

Our compile_to_instrs function now looks like this:

fn compile_to_instrs(e: &Exp) -> Vec<Instr> {
  match e {
    Exp::Num(n) => vec![ Instr::Mov(Reg::Rax, *n)],
    Exp::Add1(e) => {
      /* ?? */
    }
    Exp::Sub1(e) => {
      /* ?? */
    }
  }
}

Do Now!

Try to complete this scaffolding yourself.

The key observation in the hand-written assembly above is that our translations are compositional, that is, they recur on their subpieces, and a translation of a composite expression is simply a function of the translations of its pieces. Moreover, we know that constants always wind up in rax, and add1 mutates in place, which means that our answers will always be in rax as desired. So our compiler for this language is

fn compile_to_instrs(e: &Exp) -> Vec<Instr> {
  match e {
    Exp::Num(n) => vec![ Instr::Mov(Reg::Rax, *n)],
    Exp::Add1(e) => {
      let mut is = compile_to_instrs(e);
      is.push(Instr::Mov(Reg::Rax, 1))
      is
    }
    Exp::Sub1(e) => {
      let mut is = compile_to_instrs(e);
      is.push(Instr::Mov(Reg::Rax, -1))
      is
    }
  }
}

2.5 Testing

Do Now!

Run the given source programs through our compiler pipeline. It should give us exactly the handwritten assembly we intend. If not, debug the compiler until it does.

Exercise

Extend this language with a new operation: double(expr) should produce twice the value of the inner expression. Go through the five stages above: concrete syntax, examples, abstract syntax, transformation, and tests. Do we need any new features of the compiler pipeline, or of assembly, in order to achive this? What if the operation were halve(expr) instead?

Exercise

There are other assembly instructions we could have added to our output language. The sub instruction is the counterpart to add, but performs subtraction instead. The inc and dec instructions specifically add or subtract 1. Enhance our definition of Instr to include one or more of these new instructions, and modify compile_to_instrs (and any other functions necessary) to take advantage of them.

3 Growing the language: adding let

As above, every time we enhance our source language, we need to consider several things:

1. Its impact on the concrete syntax of the language

2. Examples using the new enhancements, so we build intuition of them

3. Its impact on the abstract syntax and semantics of the language

4. Any new or changed transformations needed to process the new forms

5. Executable tests to confirm the enhancement works as intended

3.1 The new syntax, both concrete and abstract

Let’s grow the language above further, by adding the concepts of identifiers and let-bindings:

‹expr›: ... | IDENTIFIER | let IDENTIFIER = ‹expr› in ‹expr›

and its corresponding abstract syntax

enum Exp {
  ...
  Id(String),
  Let(String, Box<Exp>, Box<Exp>)
}

3.2 Examples and semantics

Do Now!

Extend the interpreter from above to handle the new constructs in this language. You will need a function with signature

interpret(&Exp) -> i64

...and you will certainly need a helper function. What should that function do, and what should its signature be?

Writing this interpreter is straightforward, at least initially: numbers evaluate to themselves, and adding or subtracting one from an expression should simply evaluate the expression and then add or subtract one from the result. But what should we do about identifiers and let-bindings?

Something needs to keep track of what each identifier currently means, which implies we need an environment. The type of that environment leads to two “obvious” design choices: we could match each identifier to the expression that it was bound to, leading to an environment of type [(&str, Exp)], or we could match each identifier to the result of evaluating that expression, leading to an environment type of [(&str, i64)]. In this language, there is no distinction in meaning between the two — every program will compute the same number. But, for a more complicated language, there could be massive differences in performance or even meaning.

Do Now!

Suppose we added an infix Plus(Box<Exp>, Box<Exp>) operation. Construct a program whose running time is drastically worse with the first environment type, compared to the second environment type.

Suppose we added an expression Print(Box<Exp>) that both prints its argument to the console, and evaluates to the same value as its argument. Construct a program whose behavior is actually different with the two environment types.

The former environment type leads to what’s known as lazy behavior, where an identifier is evaluated to a result on demand, while the latter environment type leads to what’s known as eager behavior, where an expression is fully evaluated before being bound to an identifier, and never needs to be evaluated again.

Once we have the notion of an environment, interpreting let and identifiers is easy: the former extends the environment, and the latter looks up the identifier name in the environment. But is it really that simple?

As soon as we introduce names and bindings, we have to contend with the notion of scope, that is, which names are available for use within any given expression. Let us declare that the intended meaning of let x = e1 in e2 is such that x can be used in the second expression, but cannot be used in the first one. So one potential meaningless program in our language would be let x = 5 in add1(y).

Exercise

Are there other potential forms of failure for our current language? Explain them, if any.

We need to decide on a semantics for multiple bindings of the “same name”: what should the program let x = 1 in let x = 2 in x mean? We could decree that such a program is simply in error, but it is more convenient to decide that it evaluates to 2, that is, inner bindings shadow outer ones.

Now that we know what our programs are supposed to mean, let’s try to compile them instead of interpreting them. For now, let’s assume that scoping errors cannot happen; we’ll need to revisit this faulty assumption and ensure it later.

4 The stack

Immediately, we can see two key challenges in compiling this code: in the little fragment of assembly that we currently know, we have no notion of “identifier names”, and we certainly have no notion of “environments”. Worse, we can see that a single register can’t possibly be enough, since we may need to keep track of several names simultaneously.2To be fair, this language is simple enough that we actually don’t really need to; we could optimize it easily such that it never needs more than one. But as such optimizations won’t always work for us, we need to handle this case more generally. So how can we make progress? One key insight is to broaden what we think of when considering names. In our interpreter, a name was used to look up what value we meant. But realistically, any unique identifier will suffice, and all our values will ultimately need to exist somewhere in memory at runtime. Therefore we can replace our notion of a name is a string with a name is a memory address. This leads to our second key insight: during compilation, we can maintain an environment of type Vec<&str, Address> (for some still-to-be-determined type Address). We can extend this environment with new addresses for new identifiers, each time we compile a let-binding, and we can look up the relevant address every time we compile an identifier. Once we’ve done so, we don’t need this environment at runtime — its contents have been used in the construction of the compiled output, and therefore we don’t need to maintain this structure any further. This eliminates both of our representation problems (of how to encode string names and the whole environment), but raises a new question: how do we assign addresses to identifiers in a sufficient way?

To make any further progress, we need to know a little bit about how memory is used in programs. Memory is conceptually just a giant array of bytes, addressed from 0 to 264 (on 64-bit machines). There are restrictions on which addresses can be used, and conventions on how to use them appropriately. Programs don’t start at memory address 0, or at address 264, but they do have access to some contiguous region:

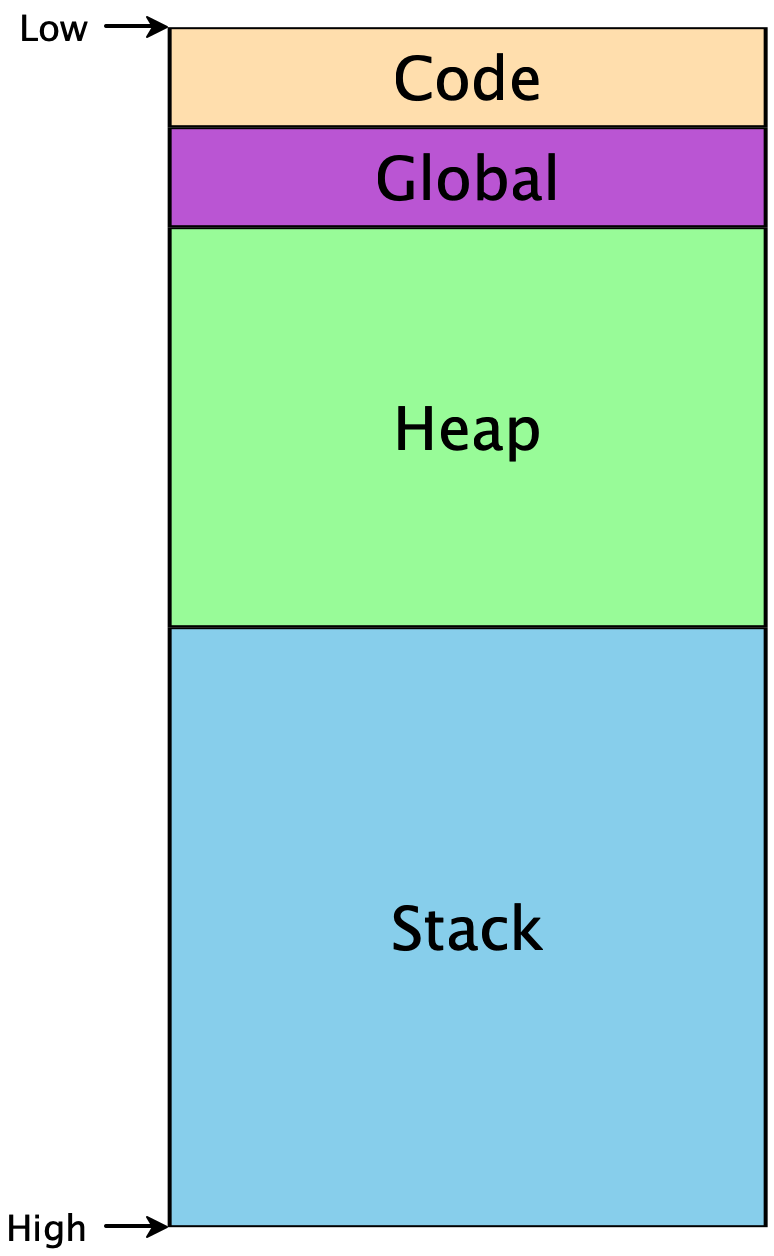
The Code segment includes the code for our program. The Global segment includes any global data that should be available throughout our program’s execution. The Heap includes memory that is dynamically allocated as our program runs — we’ll come back to using the heap later. Finally the Stack segment is used as our program calls functions and returns from them — we’ll need to work with this segment right away.

Because the heap and the stack segments are adjacent to each other, care must be taken to ensure they don’t actually overlap each other, or else the same region of memory would not have a unique interpretation, and our program would crash. This implies that as we start using addresses within each region, one convenient way to ensure such a separation is to choose addresses from opposite ends. Historically, the convention has been that the heap grows upwards from lower addresses, while the stack grows downward from higher addresses.3This makes allocating and using arrays particularly easy, as the ith element will simply be i words away from the starting address of the array.

The stack itself must conform to a particular structure, so that functions can call each other reliably. This is (part of) what’s known as the calling convention, and we’ll add more details to this later. For now, the high-level picture is that the stack is divided into stack frames, one per function-in-progress, that each stack frame can be used freely by its function, and that when the function returns, its stack frame is freed for use by future calls. (Hence the appropriateness of the name “stack”: stack frames obey a last-in-first-out discipline as functions call one another and return.) When a function is called, it needs to be told where its stack frame begins. Per the calling convention, this address is stored in the rsp register (short for “stack pointer”)4This is a simplification. We’ll see the fuller rules soon.. Addresses lower than rsp are free for use; addresses greater than rsp are already used and should not be tampered with:

5 Allocating identifiers on the stack

The description above lets us refine our compilation challenge: we have an arbitrary number of addresses available to us on the stack, at locations RSP - 8 * 1, RSP - 8 * 2, ... RSP - 8 * i. (The factor of 8 comes because we’re targeting 64-bit machines, and addresses are measured in bytes.) Therefore:

Exercise

Given the description of the stack above, come up with a strategy for allocating numbers to each identifier in the program, such that identifiers that are potentially needed simultaneously are mapped to different numbers.

5.1 Attempt 1: Naive allocation

One possibility is simply to give every unique binding its own unique integer. Trivially, if we reserve enough stack space for all bindings, and every binding gets its own stack slot, then no two bindings will conflict with each other and our program will work properly.

In the following examples, the code is on the left, and the mappings of names to stack slots is on the right.

   let x = 10       /* [] */
in add1(x)          /* [ x --> 1 ] */

   let x = 10       /* [] */
in let y = add1(x)  /* [x --> 1] */
in let z = add1(y)  /* [y --> 2, x --> 1] */
in add1(z)          /* [z --> 3, y --> 2, x --> 1] */

   let a = 10             /* [] */
in let c =    let b = add1(a)   /* [a --> 1] */
           in let d = add1(b)   /* [b --> 2, a --> 1] */
           in add1(b)           /* [d --> 3, b --> 2, a --> 1] */
in  add1(c)               /* [c --> 4, d --> 3, b --> 2, a --> 1] */

We can implement this strategy fairly easily: simply keep a global mutable counter of how many variables have been seen, and a global mutable table mapping names to counters. But as the last example shows, this is wasteful of space: in the final line, neither b nor d are in scope, but their stack slots are still reserved. As programs get bigger, this would be very inefficient.

An equally important, though much subtler, problem is the difficulty of testing this implementation. We would expect that compile_to_instrs should be a deterministic function, and that compiling the same program twice in a row should produce identical output. But because of mutable state, this is not true: the second time through, our global counter has been incremented beyond its initial value, so all our stack slots will be offset by an unwanted amount. We could try to resolve this by having some way to “reset” the counter to its initial value, but now we have two new hazards: we have to remember to reset it exactly when we mean to, and we have to remember not to reset it at any other time (even if it would be “convenient”). This is an example of the singleton anti-pattern: having a single global value is almost always undesirable, because you often want at least two such values — one for the answer and one for testing — and you’ll likely want more than that, eventually. Additionally, as our compilers get more complex, we’d have more and more such mutable variables to remember to reset, and the likelihood of mistakes rises quickly.

(Anecdotally: a growing trend in compiler architecture is to design a language server, which basically takes the compiler and leaves it running as a service that can be repeatedly queried to recompile files on demand. This helps amortize the increasingly large startup cost of sophisticated compilers, and makes it much easier to build language support for new languages into new editors. But having “compilers as a service” implies that they must be exceedingly careful of mutable state, or else subsequent compilations might produce different, potentially incorrect, results than earlier ones!)

5.2 Attempt 2: Stack allocation

A closer reading of the code reveals that our usage of let bindings also forms a stack discipline: as we enter the bodies of let-expressions, only the bindings of those particular let-expressions are in scope; everything else is unavailable. And since we can trace a straight-line path from any given let-body out through its parents to the outermost expression of a given program, we only need to maintain uniqueness among the variables on those paths. Here are the same examples as above, with this new strategy:

   let x = 10       /* [] */
in add1(x)          /* [ x --> 1 ] */

   let x = 10       /* [] */
in let y = add1(x)  /* [x --> 1] */
in let z = add1(y)  /* [y --> 2, x --> 1] */
in add1(z)          /* [z --> 3, y --> 2, x --> 1] */

   let a = 10             /* [] */
in let c =    let b = add1(a)   /* [a --> 1] */
           in let d = add1(b)   /* [b --> 2, a --> 1] */
           in add1(b)           /* [d --> 3, b --> 2, a --> 1] */
in  add1(c)               /* [c --> 2, a --> 1] */

Only the last line differs, but it is typical of what this algorithm can achieve. Let’s work through the examples above to see their intended compiled assembly forms.5Note that we do not care at all, right now, about inefficient assembly. There are clearly a lot of wasted instructions that move a value out of rax only to move it right back again. We’ll consider cleaning these up in a later, more general-purpose compiler pass. Each binding is colored in a unique color, and the corresponding assembly is highlighted to match.

   let ~hl:1:s~x =~hl:1:e~ ~hl:2:s~10~hl:2:e~
in ~hl:3:s~add1(~hl:4:s~x~hl:4:e~)~hl:3:e~

~hl:2:s~mov RAX, 10~hl:2:e~
~hl:1:s~mov [RSP - 8*1], RAX~hl:1:e~
~hl:4:s~mov RAX, [RSP - 8*1]~hl:4:e~
~hl:3:s~add RAX, 1~hl:3:e~

   let ~hl:1:s~x = 10~hl:1:e~
in let ~hl:3:s~y =~hl:3:e~ ~hl:2:s~add1(x)~hl:2:e~
in let ~hl:5:s~z =~hl:5:e~ ~hl:4:s~add1(y)~hl:4:e~
in ~hl:6:s~add1(z)~hl:6:e~

~hl:1:s~mov RAX, 10
mov [RSP - 8*1], RAX~hl:1:e~
~hl:2:s~mov RAX, [RSP - 8*1]
add RAX, 1~hl:2:e~
~hl:3:s~mov [RSP - 8*2], RAX~hl:3:e~
~hl:4:s~mov RAX, [RSP - 8*2]
add RAX, 1~hl:4:e~
~hl:5:s~mov [RSP - 8*3], RAX~hl:5:e~
~hl:6:s~mov RAX, [RSP - 8*3]
add RAX, 1~hl:6:e~

   let ~hl:1:s~a = 10~hl:1:e~
in let ~hl:5:s~c =~hl:5:e~    let ~hl:2:s~b = add1(a)~hl:2:e~
           in let ~hl:3:s~d = add1(b)~hl:3:e~
           in ~hl:4:s~add1(b)~hl:4:e~
in  ~hl:6:s~add1(c)~hl:6:e~

~hl:1:s~mov RAX, 10
mov [RSP - 8*1], RAX~hl:1:e~
~hl:2:s~mov RAX, [RSP - 8*1]
add RAX, 1
mov [RSP - 8*2], RAX~hl:2:e~
~hl:3:s~mov RAX, [RSP - 8*2]
add RAX, 1
mov [RSP - 8*3], RAX~hl:3:e~
~hl:4:s~mov RAX, [RSP - 8*2]
add RAX, 1~hl:4:e~
~hl:5:s~mov [RSP - 8*2], RAX~hl:5:e~
~hl:6:s~mov RAX, [RSP - 8*2]
add RAX, 1~hl:6:e~

Additionally, this algorithm is much easier to implement than the previous one: adding a binding to the environment simply allocates it at a slot equal to the new size of the environment. As we descend into a let-binding, we keep the current environment. As we descend into a let-body, we augment the environment with the new binding. And as we exit a let-expression, we discard the augmented environment — the bindings inside it have now fallen out of scope. Our implementation no longer needs any mutable, global state.

6 Supporting let: Implementing Attempt 2

6.1 Extending our transformations

We need to enhance our definition of registers and allow for new kinds of arguments to mov. See how can use Rust’s enums to encode the syntactic restrictions that x86-64 uses, utilizing the type system to prevent us from producing ill-formed assembly.

enum Reg {
    Rax,
    Rsp,
}

// Represents the address [ reg + 8 * offset]
struct MemRef {
    reg: Reg,
    offset: i32,
}

enum Arg64 {
     Reg(Reg),
     Imm(i64),
     Mem(MemRef)
}

enum MovArgs {
    ToReg(Reg, Arg64),
    ToMem(MemRef, Reg32),
}

enum Instr {
     Mov(MovArgs),
     Add(Reg, i32),
}

And we our type of environments can be Vec<(String, i32)>, associating variable names to their offset from rsp.

Looking up an identifier in an environment is straightforward (you implemented this for last homework). We search in reverse because we will be pushing the pairs on as we descend into the expression.

fn get(env: &[(String, i32)], x: &str) -> Option<i32> {
    for (y,n) in env.iter().rev() {
        if &x == y {
            return Some(*n);
        }
    }
    None
}

We can add a name to an environment using .push().

Now our compilation is straightforward. We sketch just the let-binding case; we leave the others as an exercise (note that we return a Result now because we might have unbound variable errors):

fn compile(e: &Exp mut env: Vec<(String, i32)>) -> Result<Vec<Instr>, String> {
   match e {
     Let(x, e1, e2) => {
       let mut is = compile(e1, env.clone())?;
       let offset = ... // Calculate the offset from env
       env.push((String::from(x), offset));
       is.push(Instr::Mov(MovArgs::ToMem(MemRef { reg: Reg::Rsp, offset: offset }), Reg::Rax));
       is.extend(compile(e2, env))?;
       Ok(is)
     }
   }
}

Exercise

Here we clone the environment when we compile the sub-expression. What are alternative approaches we could use to managing the environment that don’t use as much copying?

6.2 Testing

Exercise

Complete this compiler, and test that it works on all these and any other examples you can throw at it.

1For a little while! The details of this function will get more elaborate, and we’ll actually wrap this function in a larger pipeline, but the overall signature and purpose of the function will remain unchanged.

2To be fair, this language is simple enough that we actually don’t really need to; we could optimize it easily such that it never needs more than one. But as such optimizations won’t always work for us, we need to handle this case more generally.

3This makes allocating and using arrays particularly easy, as the ith element will simply be i words away from the starting address of the array.

4This is a simplification. We’ll see the fuller rules soon.

5Note that we do not care at all, right now, about inefficient assembly. There are clearly a lot of wasted instructions that move a value out of rax only to move it right back again. We’ll consider cleaning these up in a later, more general-purpose compiler pass.